

įolios 9v and 10r from the manuscript "Raqāʾiq al-ḥaqāʾiq fī ḥisāb ad-daraj wa-d-daqāʾiq", from the Bibliothèque nationale de France, showing lattice multiplications with old Arab numerals If the simple product lacks a digit in the tens place, simply fill in the tens place with a 0. Write their product, 10, in the cell, with the digit 1 above the diagonal and the digit 0 below the diagonal (see picture for Step 1). In this case, the column digit is 5 and the row digit is 2. After writing the multiplicands on the sides, consider each cell, beginning with the top left cell.

Then each cell of the lattice is filled in with product of its column and row digit.Īs an example, consider the multiplication of 58 with 213. The two multiplicands of the product to be calculated are written along the top and right side of the lattice, respectively, with one digit per column across the top for the first multiplicand (the number written left to right), and one digit per row down the right side for the second multiplicand (the number written top-down). Method Ī grid is drawn up, and each cell is split diagonally. It is still being taught in certain curricula today.
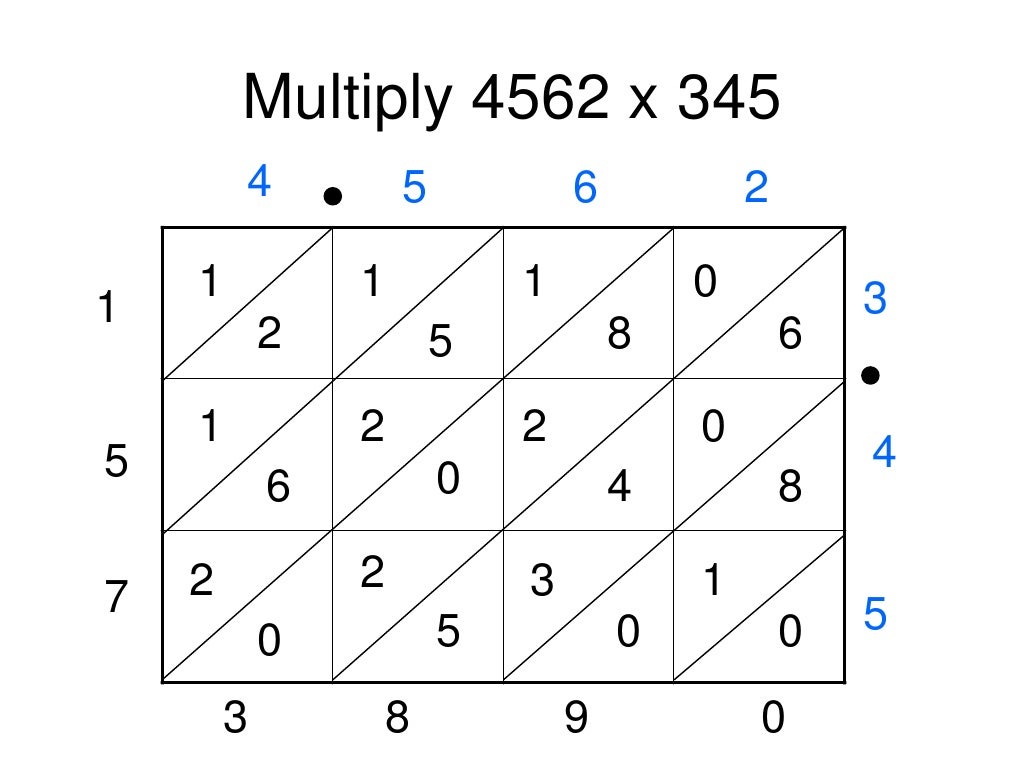
The method had already arisen by medieval times, and has been used for centuries in many different cultures. It is mathematically identical to the more commonly used long multiplication algorithm, but it breaks the process into smaller steps, which some practitioners find easier to use. Lattice multiplication, also known as the Italian method, Chinese method, Chinese lattice, gelosia multiplication, sieve multiplication, shabakh, diagonally or Venetian squares, is a method of multiplication that uses a lattice to multiply two multi-digit numbers.


 0 kommentar(er)
0 kommentar(er)
